MATEMATICA Y LAS EXPRESIONES DE LOS DESEQUILIBRIOS.

(INTENTO DE EXPRESION MATEMATICAS DEL DESEQUILIBRIO Y DEL EQUILIBRIO)

En el desarrollo del presente deseo agradecer a Agustín Caputo Bugallo, que ha realizado el proceso de formular las expresiones matemáticas de diversas temáticas.

Lo cual ha surgido mediante la colaboración e ideas que se realizaron en conjunto para concretar las expresiones del enfoque de los desequilibrios a través de expresiones matemáticas. De una extremada riqueza que se manifiestan a través de dichas iteraciones.

Se intenta dar algunos ejemplos de expresiones matemáticas que pretenden sintetizar las ideas del equilibrio y el desequilibrio. En una forma que tenga un grado de certeza tal como la expresada por los filósofos de la Academia.

Por la presente a continuación se presentan formas que trasuntan expresiones matemáticas referidas a estas situaciones:

Equilibrio absoluto 0 = 0

Equilibrios momentáneos disímiles cuantitativos t1 1=1, t2 2=2 t3= 25= 25

Desequilibrios transitorios 0,7 =! 0,9 (T0 -> T1)

1,6 =! 1,9 (T1 -> T2

Desequilibrios parciales absolutos Multivariables X_t0 =! Y_t0 , X_t1 =! Y_t1 , ……… , X_tn = ! Y_tn ; n = 0.1,……,K

Desequilibrios continuos asociados a derivadas temporales:

• Caso ascendente , derivada > 0 , X_t0 < X_t1 < X_t2 < ……. < X_tn

1 < 2 < 3 < 4 < …….< 10

• Caso descenderte, derivada < 0, X_t0 > X_t1, > X_t2 > ………> X_tn

10 > 9 > 8 > ….. > 1

• Caso mixto: Combinaciones e interpolaciones de los anteriores 10 > 8 > 5 > -10 < -9 < -8 …..

Imagen desequilibrios ondas cerebrales. Bajada.

Desequilibrios cíclicos:

Dada una secuencia de sucesos [X1, X2, X3 ,,,,,, Xn] un desequilibrios cíclico es tal que existe conexiones del tipo, X1 -> X3 , (100 -> 150)

X3 -> X4, (150 -> 200)

X4 -> X1 (200 -> 100)

En general podemos tener una combinación arbitrariamente grande de ciclos en la secuencia.

En los ciclos económicos las expresiones matemáticas no son iguales ni regulares. Sino, como expresión de las tendencias de subida y bajada hacia los puntos de inflexión.

Desequilibrios posiciones aleatorios:

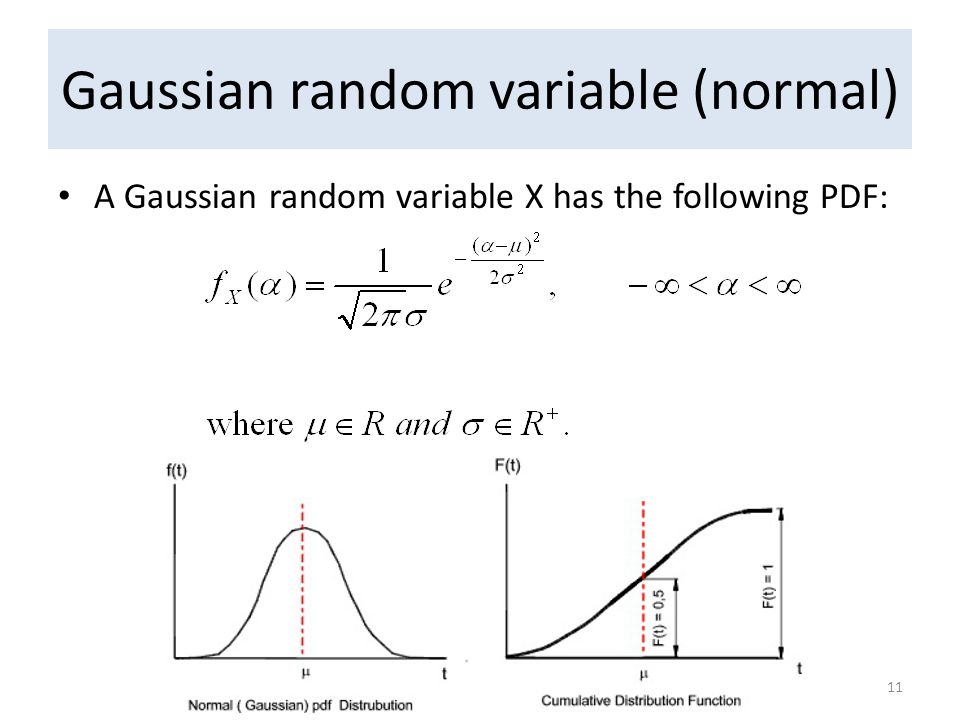
Esto se da cuando la variable o el conjunto de variables que intentamos describir son variables aleatorias (Gaussianas, tipo Poisson, etc.) de manera que solo podemos aproximarnos en una región donde se va a encontrar la variable con una cierta incerteza estadística.

300 =! 320 =! 275 =! 290 =! 200

T0 -> T1 -> T2 -> T3 -> T4

Desequilibrios permanentes absolutos:

E(tn) donde t -> + inf

E(tn) donde t -> -i inf

IDEAS DE APROXIMACIÓN A LAS DEFINICIONES DEL DESEQULIBRIO MATEMATICO.

A continuación expresaremos algunos conceptos asociados al tema.

Intentaremos definir que es un desequilibrio de manera general desde el aspecto matemático y como para caracterizar los cambios que se producen en las expresiones de los sistemas.

Sea S un sistema aislado que depende N variables internas, S(K1, K2, ….., Kn), decimos que un sistema esta equilibrio con respecto a una variable externa si y solo las derivadas de cada una de los variables internas con respecto a la variable externa son idénticamente 0.

Tomando un ejemplo concreto, una partícula libre se pude representar como un sistema S(x,y,z) donde (x,y,z) son las variables internas del sistema y una variable externa T, el tiempo. En este caso dx/dT = dy/dT = dz/dT = 0. Entonces la partícula libre esta en equilibrio realizando un movimiento uniforme rectilíneo.

Un caso más complejo es una partícula asociada a un potencial, por ejemplo, un electrón ligado a un núcleo atómico. Olvidándonos por un momento del carácter cuántico del electrón, pensemos al sistema núcleo-electrón como dos partículas de diferente carga que la otra. En este caso la fuerza electromagnética es la que rige el sistema; el electrón realiza una trayectoria elíptica alrededor del núcleo (Modelo semi-clásico) Nos podríamos preguntar, ¿si en este caso, el sistema S(x,y,z) esta en equilibrio con respecto a T?

La respuesta es no, dado que una trayectoria curva implica aceleraciones radiales y por lo tanto se da la circunstancia de la no nulidad de las derivadas temporales de las variables internas del sistema. Aun, considerando que en un sistema cerrado la energía total del sistema se conserva.

Notemos que en los dos sistemas anteriores, la energía es una cantidad conservada, por la naturaleza del sistema (sistema aislado), esto es una implicancia directa que la energía no puede crearse ni destruirse, solo transformarse. Pero, ¿Que pasa si abrimos el sistema? Consideremos dos posibles observadores, uno dentro del sistema y otro externo. Supongamos además que existe una fuerza disipativas del sistema interior al exterior que disminuye la energía del sistema interior aumentando a su vez la entropía del mismo.

El observador interior va a notar que la energía total del sistema disminuye sin razón aparente. ¿Quiere decir esto que estamos rompiendo la conservación de energía? No. Dado que el observador externo no va a notar un cambio de la energía total del sistema.

Podemos seguir extendiendo este proceso, teniendo en cuenta cada vez mas fuerzas disipativas y aumentando el tamaño del sistema. Este proceso iterativo nos lleva a la conservación de la energía para todo el universo. Como consecuencia de esto, no podemos afirmar que la energía se conserve localmente en sistemas abiertos. De manera que definiremos los desequilibrios como la interacción concatenada entre en un conjunto de sistemas abiertos.

Siguiendo este mismo análisis, podríamos estudiar que pasa con los sistemas abiertos no solo cuando los dejamos evolucionar en el tiempo. Sino cuando además cambiamos el sistema de referencia. Este concepto surge en la mecánica newtoniana donde sus leyes están claramente definidas para sistemas inerciales. Esto no implica que no podamos modelar sistemas no inerciales con sus leyes, sino que no podremos explicar fenómenos que van a surgir en la descripción del mismo, tal como las fuerzas ficticias. Las relaciones entre variables de los sistemas cuando cambiamos de sistema de referencia vienen dadas por las transformaciones galileanas.

Aun, esto es valido solo para velocidades mucho menor que la velocidad de la luz y para cuerpos macroscópicos. Dado que en su defecto deberíamos tener en cuenta consideraciones relativistas y efectos cuánticos.

¿Pero esto quiere decir que las leyes de Newton son incorrectas?

Es decir que cuando cambiamos un poco las condiciones del entorno las citadas dejan de valer?

Si y No, son dos caras de la misma moneda.

Para abordar esta pregunta debemos ahondar en el concepto de un modelo físico. Hasta ahora mencionamos los conceptos físicos, como la energía, masa, velocidad, sistemas de referencia, etc. Como si fueran realidades. Aun, así estos son abstracciones que construimos para poder cuantificar los fenómenos de la realidad y predecirlos, si es que es posible. Con cierta incerteza, tal como en la que esta involucrada en la evolución de un sistema. Un modelo físico es un conjunto de reglas, leyes o axiomas que imponemos sobre la dinámica de un conjunto de sistemas para poder describirla. Para, luego inferir su comportamiento cuando sus variables se expresan y se modifican. Bajo este concepto asumimos que la realidad es una característica subyacente. La cual fundamentalmente no podemos conocer en forma cierta.

Aun así podemos intentar medir valores asociadas a las variables de los comportamientos en los sistemas para expresar y reflejar de la mejor manera las realidades de los fenómenos. Pero es el desequilibrio la fuente de las perturbaciones. Desde el punto de vista filosófico la realidad algo inaccesible para nosotros, aun así desde el punto de vista científico, la realidad, es aquello que podemos medir y/o cuantificar. Siendo las perturbaciones las que complejizan esta proceso.

Son las incertezas experimentales las que en muchos casos alteran las expresiones de los fenómenos. Generando una barrera entre la interpretación científica de los fenómenos y la naturaleza de los mismos.

Luego de esto se podría concluir que las leyes de Newton no están bien, ni mal, sino que son validas en su entorno. Tal como la cuántica es valida en el suyo. Considerando que ambos son modelos y no realidades. Entonces, como pregunta final, podríamos formular

¿Existe el equilibrio en la naturaleza? No lo sabemos, y aunque existiera, nos es imposible medirlo con exactitud.

En este trabajo se intenta representar algunos ejemplos de expresiones matemáticas con el fin de sintetizar las ideas del equilibrio y el desequilibrio.

En tal forma que se logre con dichas referencias de un grado de certeza tal. Como la expresada por los filósofos de la Academia.

¿Si usted puede contribuir con algunas ideas al respecto se lo agradecería?

Néstor Jorge Bugallo.

28/05/2020